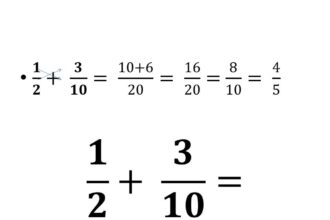- Anúncios -
O que significa frequency?
A frequência, essa onda mágica que nos envolve diariamente, é uma forma de medir a repetição de um acontecimento. Da batida do seu coração ao ritmo das estações, a frequência permeia nossas vidas como uma canção silenciosa. Descubra o significado por trás desse conceito fascinante e explore as profundezas de como a frequência molda nossa realidade.
O que significa restriction?
No mundo da linguagem e das palavras, "restriction" carrega consigo um peso interessante. Significa limitação, contensão, a imposição de restrições. É um termo poderoso que pode moldar a forma como vivemos e nos relacionamos com o mundo ao nosso redor. Explore neste artigo o significado amplo dessa palavra e como ela pode afetar diferentes áreas de nossas vidas.
O que significa cold?
O que significa "cold"? Uma palavra tão pequena, mas com um significado tão amplo. É mais do que apenas uma sensação de frio, é um estado de ânimo, uma atmosfera congelante que nos envolve. Pode ser uma expressão de distância emocional, um abismo entre duas pessoas. Também pode ser uma metáfora para a solidão e o isolamento. Uma palavra aparentemente…
Medicina
O quê significar ter compulsão alimentar?
Ah, a compulsão alimentar! Um labirinto misterioso onde o desejo voraz por…

Create an Amazing Newspaper
Siga-nos
O que significa adição?
A adição, um conceito matemático fundamental, revela-se como um enigma estimulante para…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa denominador?
Você já se perguntou o que significa denominador? Uma palavra tão peculiar…
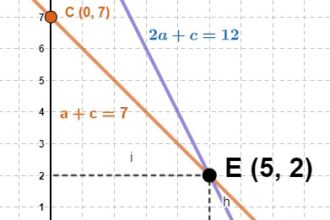
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa adição na matemática?
Quando mergulhamos no mundo da matemática, nos deparamos com diferentes termos e…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa axioma na matemática?
Você já se perguntou o que significa axioma na matemática? Bem, prepare-se…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SAT-CF-e?
Você já se perguntou o que significa SAT-CF-e? Essa sigla tem se tornado cada vez mais presente no mundo dos negócios. Neste artigo, vamos explorar o significado desse termo e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!