- Anúncios -
O que significa local?
O que significa local? Essa pequena palavra guarda consigo a capacidade de evocar sentimentos e memórias, de nos transportar para outro tempo e lugar. Local é onde nos sentimos em casa, onde as histórias são contadas e onde pertencemos. É a essência de quem somos, refletida nas ruas, nas paisagens e nas pessoas que encontramos pelo caminho. Local é mais…
O que significa least?
Você já se perguntou o significado de "least"? Essa pequena palavra em inglês pode causar confusão, mas não se preocupe, estamos aqui para desvendar seu mistério. Descubra o que significa e como usar "least" de maneira simples e eficaz.
O que significa remember?
O ato de lembrar é uma dança misteriosa entre mente e memória. É como viajar no tempo, resgatando momentos que pareciam esquecidos, revivendo sensações. Recordar é trazer à tona a essência de quem somos, conectando passado e presente. No entanto, o que significa remember vai além de simplesmente lembrar, é reconhecer a importância das memórias e o poder que têm…
Medicina
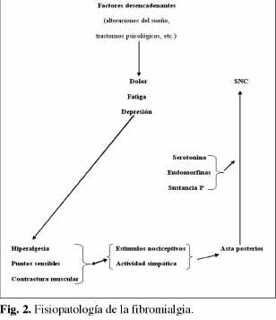
O que significa ter fibromialgia?
A fibromialgia é uma dançarina invisível que se move pelos corpos, deixando…

Create an Amazing Newspaper
Siga-nos
O que significa logaritmo na matemática?
O logaritmo, um conceito matemático tão enigmático quanto fascinante, desvenda os segredos…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…
O que significa equações irracionais?
Você já se perguntou o real significado das equações irracionais? Elas são…
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa assunto na matemática?
Matemática, a pedra angular do conhecimento numérico, muitas vezes nos desafia com…
O que significa hipotenusa?
A hipotenusa é como aquele amigo que sempre dá o suporte necessário,…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa LOL?
Você já deve ter se deparado com o termo "LOL" nas suas conversas online, mas o que exatamente isso significa? LOL é a abreviação de "Laughing Out Loud" em inglês,…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!