- Anúncios -
O que significa changing?
O que significa changing? Uma pequena palavra que guarda em si um mundo de transformações. Changing é o movimento contínuo da vida, a dança constante entre o velho e o novo. É o pulsar dos ciclos, a oportunidade de evoluir e se reinventar. É a certeza de que nada é estático, de que estamos sempre em constante mutação. Changing é…
O que significa settlement?
O significado intrínseco de settlement é tão diversificado quanto as cores de um arco-íris. Na sua essência, ele representa o elo que conecta passado e presente, marcando uma evolução constante. Seja no âmbito legal, financeiro ou social, o termo settlement engloba um universo de significados, revelando a importância das resoluções e acordos para a busca pela harmonia. Venha desvendar os…
O que significa intention?
O que significa intention? A intenção é como o farol que ilumina o caminho a ser percorrido. É o combustível que impulsiona a ação e o propósito por trás de nossas decisões. A intenção é a força invisível que define o curso da nossa jornada, guiando-nos em direção aos nossos objetivos. É o elo entre o sonho e a realidade,…
Medicina
O que significa ter alergia?
Ter alergia é ter uma dança descontrolada de células imunes no corpo.…

Create an Amazing Newspaper
Siga-nos
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…
O que significa subtração?
A subtração é um conceito matemático que pode parecer complicado à primeira…
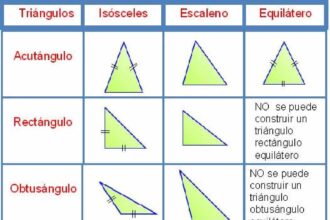
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa coeficientes?
Mergulhando no mundo dos números, nos deparamos com os misteriosos coeficientes. Esses…
O que significa multiplicação?
A multiplicação é como uma poção mágica matemática que transforma um número…
O que significa adição na matemática?
Quando mergulhamos no mundo da matemática, nos deparamos com diferentes termos e…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CT-e?
CT-e, abreviação de Conhecimento de Transporte Eletrônico, é um documento digital obrigatório para empresas que realizam transporte de carga. Essa tecnologia revolucionária simplifica a emissão e o controle dessas informações,…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!