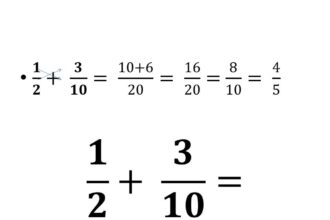- Anúncios -
O que significa approach?
Abordagem é a maneira única com a qual nos aproximamos de algo. É como um dançarino que segue o ritmo da música, adaptando seus movimentos para se encaixarem perfeitamente. É a chave para desvendar os segredos do mundo, permitindo-nos compreender de forma mais profunda e significativa. Descubra o significado do "approach" e desbrave novos caminhos em direção ao conhecimento.
O que significa flat?
O termo "flat" tem uma sonoridade suave e moderna, mas você sabe o que realmente significa? Na língua inglesa, "flat" significa apartamento, caracterizado por um espaço compacto e funcional. Agora que você já sabe, pode começar a explorar os encantos dos flats com uma nova perspectiva!
O que significa chest?
Chest, uma palavra tão simples, mas com tantos significados. Na língua inglesa, pode se referir ao peito, à caixa ou até mesmo a um jogo de tabuleiro. Então, qual será o contexto? Descubra o significado por trás dessa palavra intrigante neste artigo.
Medicina
O que significa fissura anal ou fístula anal?
Você já ouviu falar de fissura anal ou fístula anal? Embora possam…

Create an Amazing Newspaper
Siga-nos
O que significa álgebra?
Um mundo de incógnitas e equações complexas, álgebra é um ramo fascinante…
O que significa denominador?
Você já se perguntou o que significa denominador? Uma palavra tão peculiar…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…
O que significa quociente?
O que significa quociente? Uma pergunta que pode desencadear diversos pensamentos profundos…
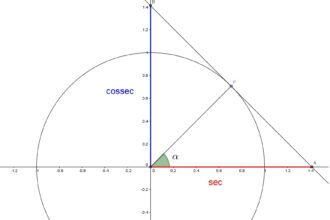
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa expressão numérica?
A expressão numérica, um enigma matemático envolto em símbolos, números e operações.…
O que significa assunto na matemática?
Matemática, a pedra angular do conhecimento numérico, muitas vezes nos desafia com…
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa HIV?
O HIV, também conhecido como Vírus da Imunodeficiência Humana, é um termo que carrega consigo um peso significativo. Por trás dessas três letras está uma realidade complexa, capaz de despertar…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!