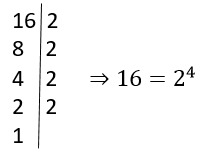- Anúncios -
O que significa dominant?
Você já se perguntou o que significa "dominant"? Essa palavra pode ter diferentes significados, dependendo do contexto em que é utilizada. Descubra mais sobre essa palavra intrigante e amplie seu vocabulário de forma divertida e educativa.
O que significa call?
Na linguagem dos investimentos, "call" refere-se à opção de compra de um ativo por um preço pré-determinado. É uma estratégia comum no mercado financeiro para proteger posições ou lucrar com a valorização de determinados ativos.
O que significa rubio em Espanhol?
Você já se perguntou o que a palavra "rubio" significa em espanhol? Essa curiosa palavra se refere a algo ou alguém com cabelos loiros ou ruivos. Então, se você está aprendendo espanhol e se deparar com o termo "rubio", agora já sabe o que ele significa!
Medicina
Qual o tempo de afastamento do CID M54?
Afastamento por tempo de CID M54: O que você precisa saber Quando…

Create an Amazing Newspaper
Siga-nos
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…
O que significa escalar na matemática?
Você já se perguntou o que significa escalar na matemática? Bem, imagine-se…
O que significa hipotenusa?
A hipotenusa é como aquele amigo que sempre dá o suporte necessário,…
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa IMHO?
Você já se deparou com a sigla "IMHO" nas redes sociais e não faz ideia do que ela significa? Não se preocupe, vamos explicar tudo para você! IMHO é a…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!