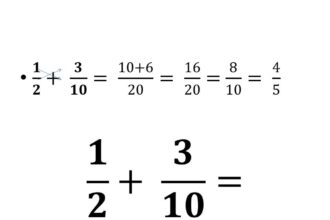- Anúncios -
O que significa cream?
Cream é uma palavra em inglês que significa creme em português. Pode ser utilizado em diferentes contextos como culinária, beleza e moda. Descubra mais sobre suas aplicações e significados!
O que significa what is your name?
Nomes são fragmentos de identidades. Uma frase aparentemente simples, 'O que significa 'What is your name?' em português?', nos conduz a um universo de heranças culturais e linguísticas. Descubra como um questionamento aparentemente trivial pode abrir portas para compreender quem somos.
O que significa beat?
O termo "beat" tem origem na cultura americana dos anos 50 e representa uma geração de escritores e artistas que buscavam a liberdade criativa. Atualmente, é utilizado para descrever um estado de espírito ou estilo de vida despojado e autêntico.
Medicina
O que significa ter dengue?
Ter dengue é como ser agredido por uma horda de mosquitos invisíveis.…

Create an Amazing Newspaper
Siga-nos
O que significa geometria na matemática?
Geometria, uma palavra que desperta curiosidade e desafia a imaginação. Na matemática,…
O que significa equação?
O que significa equação? Quando mergulhamos no universo da matemática, nos deparamos…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…
O que significa função afim na matemática?
A função afim na matemática é como uma dança matemática encantadora, na…
O que significa matriz na matemática?
Matriz, um conceito tão simples, mas tão profundo. Como uma teia intrincada…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa seno na matemática?
O seno, um dos mais enigmáticos termos da matemática, desperta curiosidade e…
O que significa isósceles?
O que significa isósceles? Essa palavra enigmática carrega consigo mistérios geométricos e…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
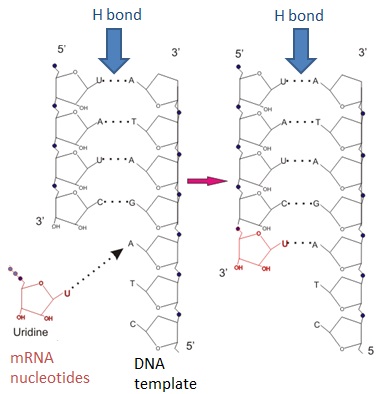
O que significa RNA?
Se você olhar para a própria essência da vida, vai se deparar com o RNA. Essas três letras representam uma das moléculas mais fundamentais e intrigantes da biologia. Mas o…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!