- Anúncios -
O que significa classic?
O que significa classic? Essa palavra tão versátil e cheia de significados tem o poder de nos transportar para épocas passadas, evocando elegância, sofisticação e tradição. Classic é um adjetivo que descreve algo, seja uma peça de roupa, um objeto de decoração ou um estilo arquitetônico, que é atemporal, intemporal, que transcende modismos e permanece relevante ao longo dos anos.…
O que significa west?
O que significa west? Uma pergunta aparentemente simples, mas com um significado que vai além de uma simples direção geográfica. O 'oeste' carrega consigo o conceito de horizonte, de conquista e de novos caminhos a serem desbravados. É a busca pelo desconhecido, a coragem de explorar e a esperança de um futuro promissor.
O que significa minor?
O termo "minor" é uma expressão que possui diversos significados e interpretações, dependendo do contexto em que é utilizado. Desde uma referência à idade até uma reflexão sobre a importância da diversidade e inclusão, o significado de "minor" pode ser tão vasto quanto nossa imaginação permite. Descubra mais sobre esse termo intrigante e como ele influencia nossas percepções e relações…
Medicina
O que significa epilepsia?
A palavra "epilepsia" carrega consigo um mistério e uma complexidade que muitas…

Create an Amazing Newspaper
Siga-nos
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…
O que significa isósceles?
O que significa isósceles? Essa palavra enigmática carrega consigo mistérios geométricos e…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…
O que significa assunto na matemática?
Matemática, a pedra angular do conhecimento numérico, muitas vezes nos desafia com…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…
O que significa média na matemática?
Você já se perguntou o que significa média na matemática? A média…
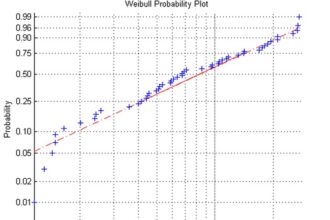
O que significa probabilidade na matemática?
A probabilidade sempre nos desafia com seu mistério matemático. Ela é um…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa EPI?
O que significa EPI? Descubra o mundo além das siglas e mergulhe em um universo de proteção e segurança. Os Equipamentos de Proteção Individual são a chave para garantir a…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!