- Anúncios -
O que significa decline?
O decline é como uma dança, um movimento gracioso em que nos afastamos lentamente de algo. É uma palavra que carrega consigo o peso da despedida, a tristeza da perda, mas também a promessa de renovação e recomeço. É a arte de deixar para trás o que não serves mais, de abrir espaço para o novo. No entanto, decline também…
O que significa average?
O que significa average? Essa palavrinha aparentemente simples pode ter um significado bem mais profundo do que imaginamos. Ela representa uma medida de tendência central, que equilibra extremos e nos traz a noção do valor típico. É a essência da média, o ponto de equilíbrio entre os altos e baixos. Mas vai além disso, average pode ser uma metáfora para…
O que significa right?
Você já se perguntou qual o significado da palavra "right"? Neste artigo, vamos explorar esse termo em diferentes contextos e descobrir como ele pode ser interpretado de maneiras distintas. Então prepare-se para ampliar o seu conhecimento sobre essa pequena palavra com um grande significado.
Medicina

Create an Amazing Newspaper
Siga-nos
O que significa equação logarítmica?
Você já ouviu falar sobre equações logarítmicas? Essas expressões misteriosas podem parecer…
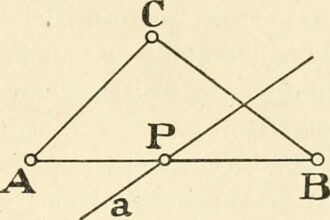
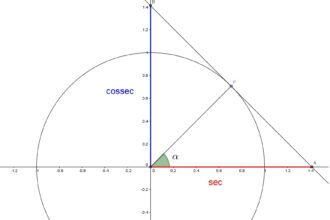
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa fórmula de Bhaskara na matemática?
A fórmula de Bhaskara, na matemática, é um marco que transcende a…
O que significa vetor na matemática?
Quando entramos no mundo da matemática, nos deparamos com diversos conceitos e…
O que significa teorema?
O teorema, um termo comumente usado na matemática, é como uma joia…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…
O que significa acumulação na matemática?
A acumulação é um conceito matemático fascinante que nos permite entender o…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa FYI?
Sem dúvida, a sigla FYI já deve ter aparecido na sua caixa de entrada ou nas redes sociais. Mas o que ela realmente significa? FYI, abreviação de "for your information",…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!