- Anúncios -
O que significa additional?
Você já se perguntou o que significa "additional"? Essa palavra em inglês pode ter diferentes significados em português, como "adicional", "extra" ou "suplementar". Descubra mais sobre o uso e as nuances dessa palavra e aprimore seu vocabulário em português.
O que significa historic?
O que significa histórico? Essa é uma pergunta que nos leva a explorar as profundezas do tempo, resgatar memórias e compreender a importância do passado. É uma palavra que guarda em si a grandiosidade das conquistas, o peso das tragédias e a moldura de um mundo em constante transformação. Historic é história viva, é olhar para trás e compreender que…
O que significa cloud?
Nuvem, um termo que transcende o olhar para o céu. Mas afinal, o que significa cloud? Um conceito que desafia a gravidade, trazendo a capacidade de armazenar e acessar dados remotamente. Uma verdadeira revolução que nos permite voar pelas barreiras físicas e mergulhar em um mundo infinito de possibilidades. A nuvem, agora mais do que nunca, está ao nosso alcance.
Medicina
O que significa doença pulmonar obstrutiva crônica?
Doença Pulmonar Obstrutiva Crônica (DPOC) é um termo que assombra muitas pessoas,…

Create an Amazing Newspaper
Siga-nos
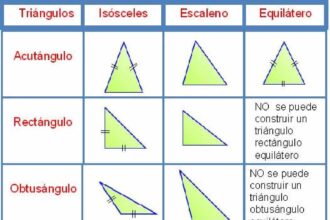
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
O que significa isósceles?
O que significa isósceles? Essa palavra enigmática carrega consigo mistérios geométricos e…
O que significa algoritmo?
Você já ouviu falar em algoritmo, mas sabe o que isso realmente…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa dividendo?
Você já se perguntou o que significa dividendo? Essa é uma palavrinha…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SA?
Você já se deparou com a sigla "SA" e não faz ideia do que significa? Não se preocupe! Neste artigo, vamos explorar o significado dessa expressão de forma criativa, desvendando…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!