- Anúncios -
O que significa violation?
Violations- palavras que ecoam com um peso desconcertante. Mas o que significa realmente "violation"? Na língua portuguesa, essa palavra representa a transgressão de limites, a quebra de regras e o desrespeito aos direitos. Ela carrega consigo a dor de quem sofreu injustiças, mas também nos motiva a lutar pelo que é correto. Ao compreender o significado de "violation", abrimos caminho…
O que significa guard?
Você já se perguntou o que significa a palavra "guard"? Essa pequena palavra, tão simples em sua aparência, carrega consigo diversos significados. Do ato de proteger até o sentido de vigilância, o termo "guard" possui um grande poder simbólico. Acompanhe neste artigo uma exploração criativa sobre o significado por trás dessa palavra.
O que significa onion?
A palavra "onion" é um dos mistérios que ronda a língua inglesa. Com um som engraçado e uma forma peculiar, o significado por trás dessa simpática palavra é tão básico quanto a sua aparência: cebola. Mas como algo tão simples pode ter um nome tão intrigante? Neste breve artigo, mergulhamos na história e etimologia dessa palavra, desvendando o mistério por…
Medicina
O que significa ter tuberculose?
O que significa ter tuberculose? Uma simples palavra que carrega consigo uma…

Create an Amazing Newspaper
Siga-nos
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
O que significa aceleração na matemática?
A aceleração, na matemática, é um conceito fundamental que nos permite entender…
O que significa algarismo na matemática?
O que significa algarismo na matemática? Quando nos deparamos com essa palavra…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
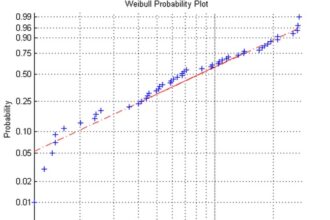
O que significa probabilidade na matemática?
A probabilidade sempre nos desafia com seu mistério matemático. Ela é um…
O que significa denominador?
Você já se perguntou o que significa denominador? Uma palavra tão peculiar…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa álgebra?
Um mundo de incógnitas e equações complexas, álgebra é um ramo fascinante…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CSOSN?
O CSOSN, sigla para "Código de Situação da Operação no Simples Nacional", é um importante conceito para entender a tributação das empresas enquadradas no Simples Nacional. Mas afinal, o que…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!