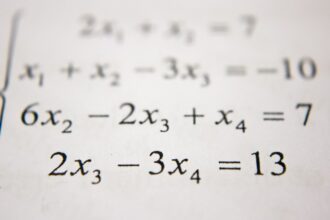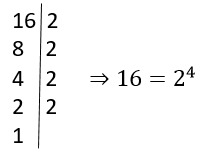- Anúncios -
O que significa coat?
O que significa coat?" é uma pergunta que pode despertar curiosidade nos novatos da língua inglesa. Um coat, de forma resumida, é uma peça de vestuário que nos mantém aquecidos e estilosos. Mas por trás dessa palavra aparentemente simples, há uma história rica e interessante a ser desvendada. Neste artigo, exploraremos suas origens, diferentes tipos de coats e como eles…
O que significa performance?
A performance, embora abstrata, é uma manifestação de arte que transcende o discurso. Ela é a dança enigmática entre corpo e espaço, expressão e interpretação, onde artistas ousam explorar limites e provocar emoções. Ela desafia convenções e convida o público a embarcar em uma jornada única, onde o inexplicável se torna tangível. A performance é a reinvenção das regras, um…
O que significa tragedy?
Você já se perguntou o que realmente significa a palavra "tragédia"? Na sua essência, a tragédia é uma forma de arte que se baseia na representação dos sofrimentos humanos. Uma experiência intensa e complexa, capaz de despertar emoções profundas no espectador. Mas o que torna uma situação uma verdadeira tragédia? Descubra neste artigo o significado e as nuances dessa poderosa…
Medicina
O quê significar ter bulimia?
A bulimia é uma dança diária entre a liberdade e o aprisionamento.…

Create an Amazing Newspaper
Siga-nos
O que significa função afim na matemática?
A função afim na matemática é como uma dança matemática encantadora, na…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa vetor na matemática?
Quando entramos no mundo da matemática, nos deparamos com diversos conceitos e…
O que significa algoritmo?
Você já ouviu falar em algoritmo, mas sabe o que isso realmente…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa média na matemática?
Você já se perguntou o que significa média na matemática? A média…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…
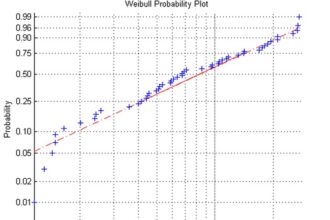
O que significa probabilidade na matemática?
A probabilidade sempre nos desafia com seu mistério matemático. Ela é um…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa MDF-e?
O MDF-e, ou Manifesto Eletrônico de Documentos Fiscais, é um elo tecnológico essencial para a logística das operações de transporte de carga no Brasil. Ao unificar e eletronicamente registrar informações…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!