- Anúncios -
O que significa satisfy?
Satisfazer, um verbo que transcende palavras e mergulha no âmago das nossas experiências mais profundas. É a sensação de plenitude, de contentamento, de ser preenchido de maneira gratificante. É aquele sorriso que nasce naturalmente, e o suspiro de alívio que escapa dos lábios. Mas, afinal, o que significa satisfazer? Vamos explorar esse universo enigmático de significados e buscar compreender as…
O que significa stranger?
Misterioso, intrigante, enigmático. Quando nos deparamos com alguém desconhecido, surge a pergunta: O que significa Stranger? Mais do que simplesmente um estranho, essa palavra carrega consigo tanto mistério quanto possibilidades. Exploraremos a essência desse termo e revelaremos como um encontro inesperado pode transformar nossas vidas de maneiras surpreendentes.
O que significa absolute?
O que significa "absolute"? Essa palavra carrega consigo um poder imenso, uma força que transcende os limites da compreensão humana. Ela evoca a ideia de algo incontestável, indiscutível, que não pode ser abalado ou questionado. É a certeza absoluta, a pureza que reside no âmago de tudo o que é real e verdadeiro.
Medicina
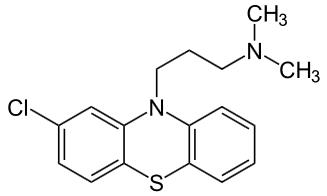
Qual o tempo de afastamento do CID M54?
Afastamento por tempo de CID M54: O que você precisa saber Quando…

Create an Amazing Newspaper
Siga-nos
O que significa escalar na matemática?
Você já se perguntou o que significa escalar na matemática? Bem, imagine-se…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…
O que significa equações polinomiais?
Você já se perguntou sobre o significado das equações polinomiais e como…
O que significa seno na matemática?
O seno, um dos mais enigmáticos termos da matemática, desperta curiosidade e…
O que significa equilátero?
No mundo da geometria, a palavra "equilátero" evoca harmonia, perfeição e equidade.…
O que significa integral na matemática?
Você já se perguntou o que realmente significa "integral" na matemática? É…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa OMG?
Você já se perguntou o que significa OMG? A expressão, que nasceu nos meios virtuais, ganhou popularidade ao invadir as conversas cotidianas. OMG é a abreviação da expressão em inglês…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!