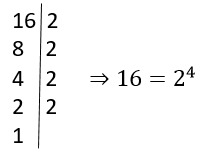- Anúncios -
O que significa young?
O que significa young? A palavra "young" vem do inglês e significa jovem. No entanto, seu significado vai além da idade. É um estado de espírito, uma energia efervescente e uma sede de descoberta. Ser young é abraçar a juventude interior, independentemente da idade cronológica. É acreditar que a vida está cheia de possibilidades, que os sonhos podem se tornar…
O que significa reject?
Rejeitar, um termo simples em aparência, porém carregado de significados profundos. Quando alguém diz "rejeito", suas palavras ecoam como muralhas, impedindo a entrada de ideias, sentimentos ou possibilidades. Porém, nesse mundo cheio de rejeições, há esperança: a de aprender a acolher o diverso, a enxergar a beleza na diferença e a rejeitar o ato de rejeitar.
O que significa assault?
Explorando as nuances da língua portuguesa, mergulhamos no significado da palavra 'assault'. Não se trata apenas de violência, mas de um ato indesejado, invasivo. Vamos desvendar seu significado e entender como ela se encaixa no contexto jurídico e social. Acompanhe-nos nessa jornada de descobertas e aprendizado linguisticamente enriquecedor.
Medicina
O que significa talassemia?
A talassemia é um termo desconhecido para muitos, mas para aqueles que…

Create an Amazing Newspaper
Siga-nos
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
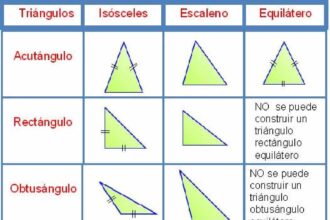
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa adição?
A adição, um conceito matemático fundamental, revela-se como um enigma estimulante para…
O que significa equação diferencial na matemática?
Resolver equações diferenciais pode ser desafiador para muitos estudantes de matemática, mas…
O que significa função afim na matemática?
A função afim na matemática é como uma dança matemática encantadora, na…
O que significa algoritmo?
Você já ouviu falar em algoritmo, mas sabe o que isso realmente…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa NFSe?
Você já ouviu falar sobre NFSe, mas sabe o que significa? A sigla NFSe se refere a Nota Fiscal de Serviços Eletrônica. Mas essa não é uma nota fiscal qualquer,…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!