- Anúncios -
O que significa square?
Square é uma palavra que possui diferentes significados em diferentes contextos. Na matemática, square refere-se ao quadrado de um número. Já na arquitetura, está associada a praças ou quadrados urbanos. Descubra mais sobre o significado deste termo versátil e intrigante.
O que significa library?
A biblioteca é um tesouro de conhecimento, um refúgio para a mente inquieta. É um espaço mágico, onde as palavras ganham vida e as histórias sussurram aos ouvidos curiosos. Nela, encontramos livros que abrem portas para outros mundos e nos transportam para além da nossa realidade. A biblioteca é uma carta de amor à cultura e ao saber, um sinônimo…
O que significa double?
Você já se perguntou o que significa "double"? Esse termo pode ter diferentes significados dependendo do contexto. Seja para designar uma bebida mais forte, uma jogada no futebol ou até mesmo uma harmonia musical, o "double" é uma expressão multifacetada que merece ser explorada. Acompanhe-nos nessa jornada para descobrir o verdadeiro significado por trás desse termo tão enigmático.
Medicina
O que significa ter bronquite?
A bronquite é uma condição respiratória que pode ser um verdadeiro desafio…

Create an Amazing Newspaper
Siga-nos
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
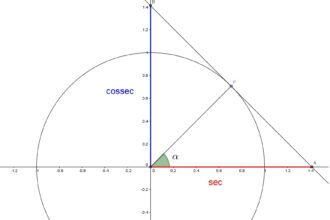
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa propriedades matemáticas?
Você já se perguntou o que significa propriedades matemáticas? Neste artigo, exploraremos…
O que significa equações irracionais?
Você já se perguntou o real significado das equações irracionais? Elas são…
O que significa equação diferencial na matemática?
Resolver equações diferenciais pode ser desafiador para muitos estudantes de matemática, mas…
O que significa atrito na matemática?
Uma sensação de hesitação e resistência surge quando dois corpos se encontram,…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa IDH?
Cada letra de "IDH" carrega um significado especial. I de Índice, D de Desenvolvimento e H de Humano. Esse indicador, famoso no mundo todo, mede o progresso de uma nação…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!