- Anúncios -
O que significa carroza em Espanhol?
O que significa carroza em espanhol?" é uma pergunta comum entre os estudantes de língua espanhola. Embora possamos imaginar uma carruagem decorada, a palavra também pode se referir a outros tipos de veículos festivos utilizados em desfiles ou festas tradicionais. Descubra mais sobre esse significado colorido e culturalmente rico da palavra "carroza" no idioma espanhol.
O que significa morning?
O que significa morning?" é uma pergunta comum entre os estudantes de inglês. A palavra "morning" em português significa "manhã", o período do dia que vai do amanhecer até o meio-dia. É uma parte importante do dia para começar com energias renovadas e positividade.
O que significa mere?
Mere. Três letras, uma infinidade de significados. Essa pequena palavra da língua portuguesa carrega consigo um mundo de possibilidades. Tão simples, porém tão complexa. Mas afinal, o que significa "mere"? Vamos explorar as camadas dessa palavra intrigante e desvendar seus segredos. Descubra se você merece o conhecimento que está por vir!
Medicina
O que significa ter esclerose múltipla?
A esclerose múltipla é uma complexa doença neurológica que afeta o sistema…

Create an Amazing Newspaper
Siga-nos
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa equações racionais?
Você já se perguntou o que significa equações racionais? Bem, essas equações…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa axioma na matemática?
Você já se perguntou o que significa axioma na matemática? Bem, prepare-se…
O que significa integral na matemática?
Você já se perguntou o que realmente significa "integral" na matemática? É…
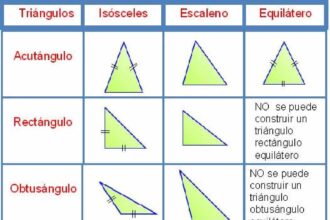
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa IDH?
Cada letra de "IDH" carrega um significado especial. I de Índice, D de Desenvolvimento e H de Humano. Esse indicador, famoso no mundo todo, mede o progresso de uma nação…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!