- Anúncios -
O que significa outside?
Espiar através da janela, sentir a brisa no rosto, explorar além dos limites conhecidos. O que significa outside? É sair da rotina, desbravar o desconhecido, conectar-se com a natureza. É a liberdade de voar longe do comum, mergulhando no mundo lá fora. É a busca por novas experiências e perspectivas. É descobrir o significado de viver plenamente.
O que significa Mrs?
Mrs. é uma forma de tratamento feminina em inglês que vem do termo "mistress". Mas o que significa essa abreviação afinal? Descubra neste artigo as origens e usos dessa palavra, que confere respeito e formalidade às mulheres. Aprenda sobre suas variantes, como "Miss" e "Ms", e como utilizá-las corretamente. Seja você uma senhora casada ou solteira, conhecer o significado de…
O que significa weapon?
A palavra "weapon" pode ter diferentes significados em diferentes contextos. No sentido literal, refere-se a qualquer objeto utilizado para atacar ou defender. Mas, metaforicamente, pode representar algo que nos ajuda ou prejudica emocionalmente. Afinal, as palavras também podem ser armas poderosas em nossas interações diárias. O importante é usá-las com cautela e responsabilidade.
Medicina
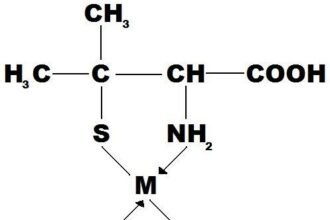
O quê significar ser transgênico?
O quê significa ser transgênico? A resposta pode ser tão profunda e…

Create an Amazing Newspaper
Siga-nos
Precisa ler
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…
O que significa associação na matemática?
Já se questionou sobre o que significa associação na matemática? Muito além…
O que significa teorema?
O teorema, um termo comumente usado na matemática, é como uma joia…
O que significa numerador?
Você já se perguntou o que significa numerador? No mundo da matemática,…
O que significa antilogaritmo na matemática?
Antilogaritmo, uma palavra intrigante no mundo da matemática. Mas o que será…
O que significa multiplicação?
A multiplicação é como uma poção mágica matemática que transforma um número…
O que significa adição na matemática?
Quando mergulhamos no mundo da matemática, nos deparamos com diferentes termos e…
O que significa área na matemática?
Na matemática, a área é um conceito fundamental que nos permite medir…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa OTAN?
A Aliança Atlântica, conhecida como OTAN, é um pacto militar que reúne diversos países do mundo ocidental. Mas afinal, o que significa OTAN? Neste artigo, vamos mergulhar nas origens e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!