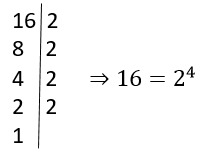- Anúncios -
O que significa identify?
O que significa identify? Essa palavra tão pequena, mas com um significado tão imenso. É como um espelho da nossa essência, capaz de revelar quem somos, nossas paixões, nossos valores. É um convite para nos conhecermos melhor, para reconhecermos nossos desejos e encontrar o nosso propósito. Identificar-se é mergulhar em si mesmo, em busca de autenticidade e conexão com o…
O que significa motivation?
Motivação é a chama interior capaz de mover montanhas, impulsionar sonhos e transformar a realidade. É a força que nos faz sair da zona de conforto e buscar incessantemente o sucesso. Mas, afinal, o que significa motivação? É o combustível da alma, é o desejo que nos impulsiona a agir, é o brilho nos olhos diante de desafios. É encontrar…
O que significa provide?
Quando nos deparamos com a palavra "provide", muitas vezes é difícil determinar seu verdadeiro significado em português. Mas pense nisso como um ato generoso de dar ou fornecer algo a alguém. É como ser um guardião confiável de algo que alguém precisa, inundando a vida do outro com cuidado e apoio.
Medicina
O que significa osteoporose?
Imagine uma teia de ossos frágeis, delicados como porcelana, que se quebram…

Create an Amazing Newspaper
Siga-nos
O que significa área na matemática?
Na matemática, a área é um conceito fundamental que nos permite medir…
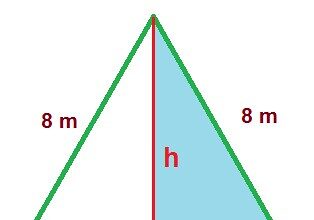
O que significa equilátero?
No mundo da geometria, a palavra "equilátero" evoca harmonia, perfeição e equidade.…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…
O que significa teorema?
O teorema, um termo comumente usado na matemática, é como uma joia…
O que significa equações polinomiais?
Você já se perguntou sobre o significado das equações polinomiais e como…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa TL;DR?
Você já se deparou com a sigla TL;DR em textos online e ficou se perguntando o que diabos isso significa? TL;DR, ou "Too Long; Didn't Read", é uma expressão utilizada…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!