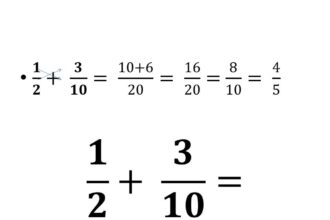- Anúncios -
O que significa skin?
A skin nada mais é do que uma extensão visual personalizada para seu dispositivo eletrônico. Ela pode ser aplicada no celular, computador, console de videogame e até mesmo em aplicativos. Elas oferecem uma forma criativa de expressão e individualidade, permitindo que você adicione um toque único ao seu dispositivo. Seja uma skin de personagem de jogo, de banda favorita ou…
O que significa okay?
Você provavelmente já ouviu a expressão "okay" em filmes, músicas ou até mesmo na conversa do dia a dia. Mas afinal, o que significa essa palavra tão comum? Neste artigo, vamos explorar o significado e a origem do "okay" e como esse termo se tornou tão universal em diversas línguas, incluindo o português.
O que significa teen?
O termo "teen" é uma abreviação da palavra em inglês "teenager", que se refere aos jovens na faixa etária entre 13 e 19 anos. Inicialmente utilizado na língua inglesa, o significado de "teen" se popularizou em todo o mundo, inclusive no Brasil, para descrever adolescentes em diferentes contextos culturais.
Medicina
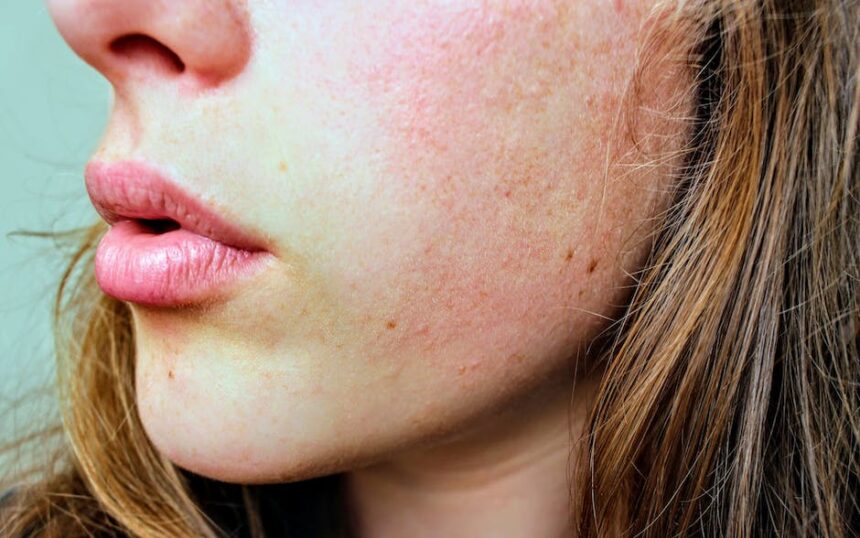
O que significa hemorroidas internas ou externas?
As hemorroidas são capazes de nos surpreender com sua presença indesejada, mas…

Create an Amazing Newspaper
Siga-nos
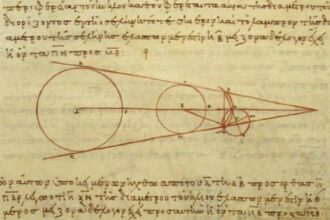
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa equação logarítmica?
Você já ouviu falar sobre equações logarítmicas? Essas expressões misteriosas podem parecer…
O que significa teorema?
O teorema, um termo comumente usado na matemática, é como uma joia…
O que significa propriedades matemáticas?
Você já se perguntou o que significa propriedades matemáticas? Neste artigo, exploraremos…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
O que significa área na matemática?
Na matemática, a área é um conceito fundamental que nos permite medir…
O que significa aproximação na matemática?
A aproximação na matemática é uma poderosa ferramenta que nos permite obter…
O que significa adição?
A adição, um conceito matemático fundamental, revela-se como um enigma estimulante para…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa ECF?
Você já se perguntou o que significa ECF? Essa sigla pode parecer um mistério, mas na verdade se refere ao Equipamento Emissor de Cupom Fiscal. Descubra como essa tecnologia revolucionou…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!