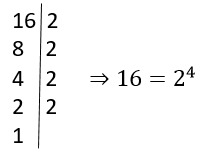- Anúncios -
O que significa project?
O que significa "project"? A palavra "project" deriva do latim "projectum" que significa algo que é lançado para a frente. No contexto atual, refere-se a um empreendimento planejado, com objetivos e prazos definidos. Pode ser utilizado em diversas áreas, como negócios, engenharia, arte e educação. Um projeto bem elaborado é capaz de transformar ideias em realidade, unindo criatividade, planejamento e…
O que significa federal?
O termo "federal" é uma palavra que carrega uma força enorme em sua essência. Significa união, colaboração e igualdade. É a garantia de que cada unidade federativa tem voz, e juntas construímos um país plural e diverso. Mas ao mesmo tempo, o federalismo também implica em uma divisão clara de competências entre União, estados e municípios. É um equilíbrio delicado…
O que significa western?
O que significa western? Este gênero cinematográfico, também conhecido como faroeste, encanta multidões com suas histórias de cowboys destemidos, duelos ao sol e paisagens de tirar o fôlego. Mas o que realmente define o western? Descubra neste artigo as características únicas desse universo narrativo que continua fascinando até os dias de hoje.
Medicina
O que significa ter síndrome metabólica?
A síndrome metabólica é um conjunto de condições que colocam sua saúde…

Create an Amazing Newspaper
Siga-nos
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…
O que significa numerador?
Você já se perguntou o que significa numerador? No mundo da matemática,…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa álgebra?
Um mundo de incógnitas e equações complexas, álgebra é um ramo fascinante…
O que significa equação diferencial na matemática?
Resolver equações diferenciais pode ser desafiador para muitos estudantes de matemática, mas…
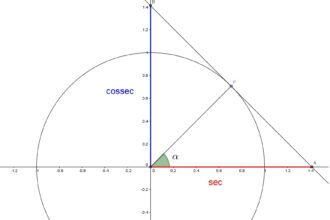
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa algarismo na matemática?
O que significa algarismo na matemática? Quando nos deparamos com essa palavra…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SUS?
O Sistema Único de Saúde, mais conhecido como SUS, é um verdadeiro guardião da saúde do povo brasileiro. Com seus princípios de universalidade, integralidade e equidade, o SUS garante acesso…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!