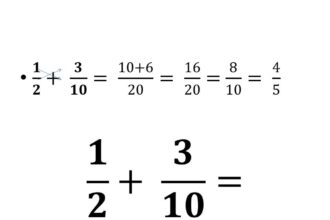- Anúncios -
O que significa trip?
Você já se perguntou o que significa a palavra "trip"? Esse termo pode ter diversos significados dependendo do contexto em que é utilizado. Descubra mais sobre essa palavra versátil e sua origem aqui.
O que significa figure?
O significado de "figure" é mais do que uma simples palavra, é uma jornada através do desconhecido. Uma figura, por vezes abstrata, é capaz de despertar nossas emoções e nos transportar para um mundo de possibilidades infinitas. Seja uma figura humana ou geométrica, ela tem o poder de se manifestar de formas únicas em cada contexto, criando um enigma que…
O que significa a expressão flesh and blood?
A expressão "flesh and blood" é frequentemente usada para descrever a ligação de sangue entre pessoas, como familiares próximos. Ela remete à ideia de conexão física e emocional entre indivíduos, destacando a importância dos laços familiares na nossa vida.
Medicina
O que significa ter síndrome de Sjögren?
Você já se perguntou o que significa ter síndrome de Sjögren? Essa…

Create an Amazing Newspaper
Siga-nos
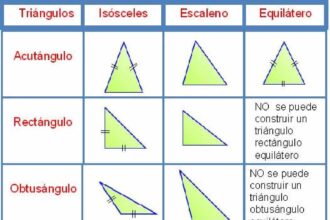
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa equilátero?
No mundo da geometria, a palavra "equilátero" evoca harmonia, perfeição e equidade.…
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa teorema?
O teorema, um termo comumente usado na matemática, é como uma joia…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CBO?
O CBO, sigla para Classificação Brasileira de Ocupações, é uma ferramenta que visa organizar e padronizar as informações sobre as ocupações do mercado de trabalho. Essa classificação traz precisão e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!