- Anúncios -
O que significa fantasy?
A fantasia é muito mais do que meras histórias imaginárias. Ela nos transporta para mundos mágicos, desperta nossa imaginação e nos faz sonhar mais alto. É um refúgio para a mente e uma fonte de inspiração para encarar a realidade. Mas afinal, o que significa fantasy? Vamos explorar essa fascinante forma de expressão e descobrir os segredos por trás das…
O que significa explore?
Explore é uma palavra carregada de curiosidade e descoberta. Significa aventurar-se em territórios desconhecidos, mergulhar em novas experiências, expandir horizontes. É um convite para desbravar o mundo e se conectar com diferentes culturas e lugares. Explore é a sensação de liberdade e a busca incessante pelo desconhecido. É deixar-se levar pela vontade de explorar e encontrar novos caminhos. Então, que…
O que significa space?
O que significa space? O termo space pode referir-se a muito mais do que um espaço físico. Ele representa liberdade, infinitas possibilidades e a capacidade de explorar o desconhecido. No entanto, também pode ser visto como uma palavra que expressa solidão, vazio ou a sensação de estar perdido. Independentemente das interpretações, space é um conceito que desperta nossa curiosidade e…
Medicina
O quê significar ser crudívoro?
Você já ouviu falar sobre o crudivorismo, mas já parou para pensar…

Create an Amazing Newspaper
Siga-nos
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa acima na matemática?
Na matemática, a palavra "acima" ganha um novo significado. Deixando de ser…
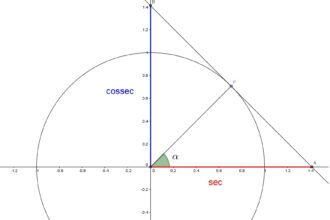
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
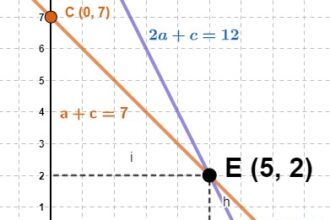
O que significa equação?
O que significa equação? Quando mergulhamos no universo da matemática, nos deparamos…
O que significa atrito na matemática?
Uma sensação de hesitação e resistência surge quando dois corpos se encontram,…
O que significa integral na matemática?
Você já se perguntou o que realmente significa "integral" na matemática? É…
O que significa numerador?
Você já se perguntou o que significa numerador? No mundo da matemática,…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa IOF?
Se você já teve a curiosidade de saber o que significa IOF, vamos esclarecer esse mistério. IOF é a sigla para Imposto sobre Operações Financeiras. Pode parecer um termo complicado,…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!