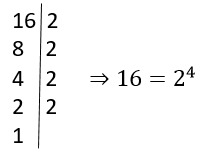- Anúncios -
O que significa privacy?
Afinal, o que significa privacy? É um termo tão extenso e complexo que fica difícil delimitar seu real significado. Alguns consideram como a proteção da intimidade, outros como o direito de controlar nossas informações pessoais. Mas, independentemente da definição exata, a privacidade é um valor fundamental que deve ser protegido em nossa sociedade moderna.
O que significa industrial?
O termo "industrial" carrega consigo uma aura de força e progresso. Representa a transformação de matérias-primas em produtos acabados, impulsionando o desenvolvimento econômico. Mas também é uma realidade complexa, onde máquinas e humanos se entrelaçam em busca da eficiência e da inovação. Industrial é um sinônimo de movimento e evolução, simbolizando a capacidade do homem de construir e moldar o…
O que significa store?
Você já se perguntou o que significa a palavra "store"? Derivada do inglês, essa palavra traz consigo uma gama de significados como comércio, loja e até mesmo armazenamento. Descubra mais sobre o fascinante mundo das stores e como elas influenciam em nosso dia a dia.
Medicina
O quê significar ser hiperlipídico?
Nosso corpo é uma máquina complexa e fascinante, e entender seus processos…

Create an Amazing Newspaper
Siga-nos
O que significa associação na matemática?
Já se questionou sobre o que significa associação na matemática? Muito além…
O que significa acumulação na matemática?
A acumulação é um conceito matemático fascinante que nos permite entender o…
O que significa área na matemática?
Na matemática, a área é um conceito fundamental que nos permite medir…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
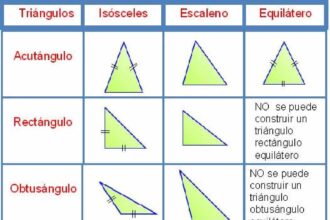
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa escalar na matemática?
Você já se perguntou o que significa escalar na matemática? Bem, imagine-se…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
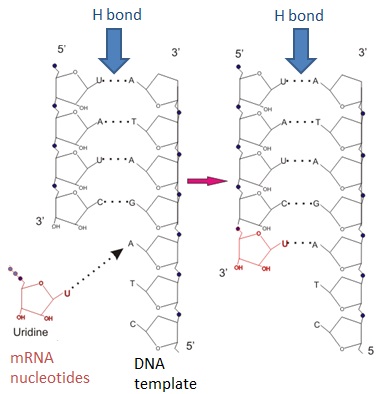
O que significa RNA?
Se você olhar para a própria essência da vida, vai se deparar com o RNA. Essas três letras representam uma das moléculas mais fundamentais e intrigantes da biologia. Mas o…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!