- Anúncios -
O que significa achieve?
Você já se perguntou qual o significado da palavra "achieve"? Bem, essa palavra pode ter vários significados, mas sua essência é a conquista, a realização. Poderíamos dizer que "achieve" é o ato de alcançar algo com sucesso, de superar obstáculos e alcançar nossos objetivos. Sejamos honestos, alcançar algo pode ser uma jornada difícil, mas a sensação de conquista no final…
O que significa recipe?
O que significa recipe?" é uma pergunta comum para muitos que estão entrando no mundo da culinária. A palavra vem do latim "recipere", que significa receber. No contexto culinário, uma receita é um conjunto de instruções que guiam a preparação de um prato específico.
O que significa tournament?
O torneio, palavra de origem latina, é uma forma de competição que desafia e estimula o espírito de competição em diversos campos. Seja no esporte, jogos de tabuleiro ou mesmo na política, os torneios são uma oportunidade de testar habilidades, conhecer novos adversários e buscar a tão almejada vitória. Mas, afinal, o que significa tournament? Descubra neste artigo tudo sobre…
Medicina
O quê significar ser detox?
A palavra "detox" está em todo lugar. Mas o que realmente significa?…

Create an Amazing Newspaper
Siga-nos
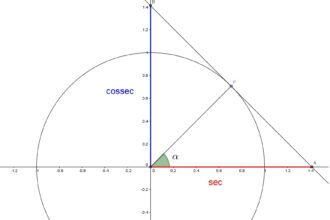
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa arco na matemática?
Na matemática, o arco é um elemento fundamental que nos leva a…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…
O que significa equações polinomiais?
Você já se perguntou sobre o significado das equações polinomiais e como…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa OTAN?
A Aliança Atlântica, conhecida como OTAN, é um pacto militar que reúne diversos países do mundo ocidental. Mas afinal, o que significa OTAN? Neste artigo, vamos mergulhar nas origens e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!