- Anúncios -
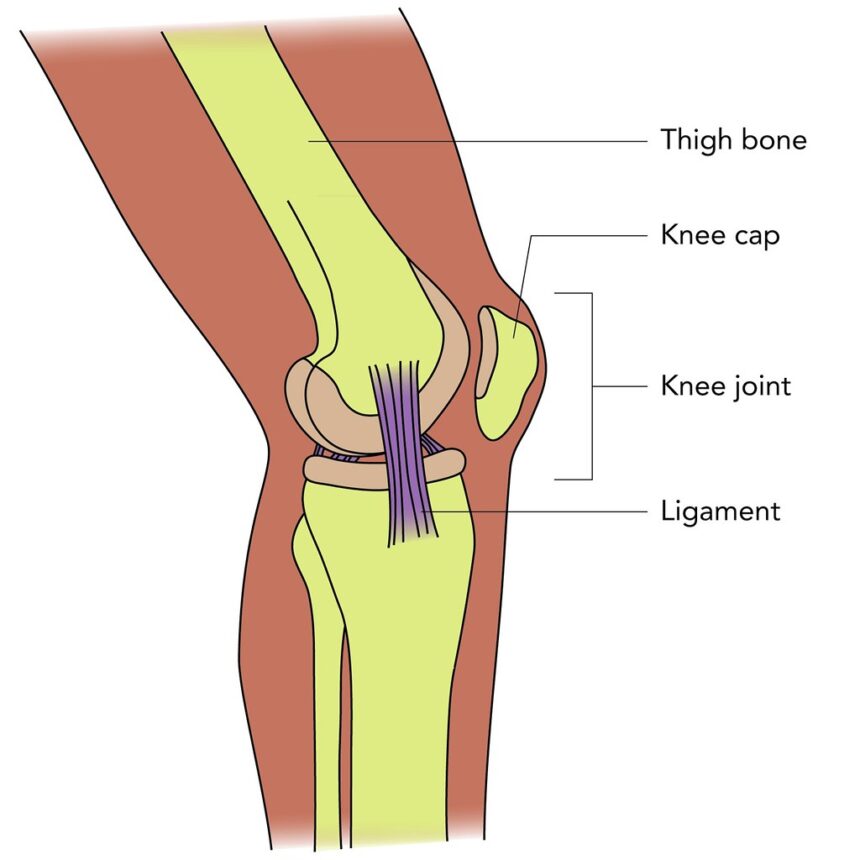
O que significa knee?
O que significa knee? Essa palavrinha curta e um tanto intrigante esconde um significado muito mais profundo. O knee é muito mais que uma junta que liga a coxa à perna. É o símbolo da mobilidade, da força e do equilíbrio. É o instrumento que nos permite caminhar, correr, pular. É a peça essencial para explorarmos o mundo e todas…
O que significa department?
O termo "department" é bastante utilizado em contexto profissional, e pode ser definido como um departamento, setor ou divisão dentro de uma organização. Representando uma área específica de responsabilidade, o department é fundamental para o funcionamento eficiente de uma empresa. Ao compreendermos o significado dessa palavra, desvendamos as engrenagens que tornam uma organização completa e harmoniosa.
O que significa scientist?
O significado da palavra "scientist" remete-nos a uma figura intrigante e curiosa. Um cientista é alguém que se dedica à exploração das maravilhas do mundo, da natureza e do conhecimento. É um explorador incansável em busca da verdade, utilizando métodos e técnicas que desvendam os mistérios que nos cercam. Um cientista está sempre sedento por descobertas, mergulhando de cabeça em…
Medicina
O que significa ter meningite?
A meningite é como uma escuridão que se instala no corpo, obscurecendo…

Create an Amazing Newspaper
Siga-nos
O que significa arco na matemática?
Na matemática, o arco é um elemento fundamental que nos leva a…
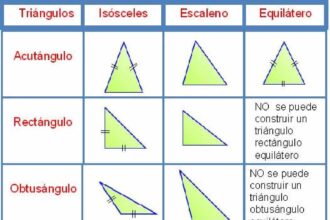
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
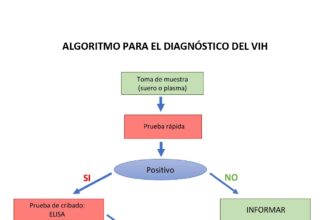
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa fórmula de Bhaskara na matemática?
A fórmula de Bhaskara, na matemática, é um marco que transcende a…
O que significa acima na matemática?
Na matemática, a palavra "acima" ganha um novo significado. Deixando de ser…
O que significa antilogaritmo na matemática?
Antilogaritmo, uma palavra intrigante no mundo da matemática. Mas o que será…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…
O que significa equações racionais?
Você já se perguntou o que significa equações racionais? Bem, essas equações…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa OMG?
Você já se perguntou o que significa OMG? A expressão, que nasceu nos meios virtuais, ganhou popularidade ao invadir as conversas cotidianas. OMG é a abreviação da expressão em inglês…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!