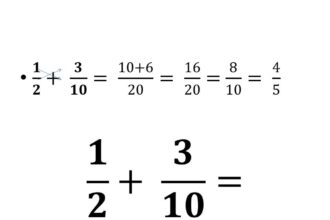- Anúncios -
O que significa big?
Já parou para pensar no que significa a palavra "big"? Embora pareça uma palavra simples, seu significado carrega uma magnitude irresistível. O "big" é imenso, é grandioso, é uma explosão de proporções gigantescas. É aquele abraço apertado, aquele sonho audacioso, aquela paixão avassaladora. É uma palavra pequena com um significado imenso, capaz de transformar o insignificante em grandioso.
O que significa win?
O que significa win? Essa pequena palavra de três letras carrega consigo um imenso poder e significado. Para alguns, win representa a vitória, o triunfo, a conquista de um objetivo. Mas talvez win também possa ser interpretado como o aprendizado em uma derrota, a resiliência diante dos desafios. Afinal, o verdadeiro significado de win será sempre subjetivo, moldado pelas experiências…
O que significa storage?
Muitos de nós já ouvimos o termo "storage", mas você já parou para pensar no seu significado real? Bem, storage é muito mais do que apenas um lugar para guardar objetos. É um tesouro escondido, onde as memórias se entrelaçam e os segredos são protegidos. É uma caixa mágica que guarda nossas histórias e nos permite revivê-las sempre que quisermos.…
Medicina
O que significa apendicite aguda?
Apendicite aguda é uma condição intrigante que muitos desconhecem. O apêndice, um…

Create an Amazing Newspaper
Siga-nos
O que significa adição na matemática?
Quando mergulhamos no mundo da matemática, nos deparamos com diferentes termos e…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
O que significa propriedades matemáticas?
Você já se perguntou o que significa propriedades matemáticas? Neste artigo, exploraremos…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa multiplicação?
A multiplicação é como uma poção mágica matemática que transforma um número…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa AIDS?
AIDS, uma cama escura onde o medo e a incerteza se encontram. Mas o que realmente significa essa sigla de pesares? Uma resposta complexa, uma doença que assombra a humanidade.…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!