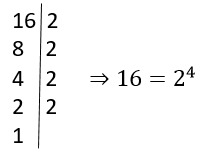- Anúncios -
O que significa run?
O que significa run? Essa pequena palavra de três letras é como um suspiro de liberdade. Ela evoca a sensação de correr pelo vento, deixando tudo para trás. Mas em inglês, 'run' pode significar muito mais: desde executar uma tarefa até administrar um negócio. Então, qual é o verdadeiro significado de 'run'? Vamos explorar essa palavra multifacetada e descobrir o…
O que significa substance?
Substance, um conceito intrínseco e multifacetado que permeia nossas vidas. É a essência que molda nosso ser, nossas ações e experiências. Seja ela física ou metafórica, a substância nos conecta ao âmago da existência, nos desafiando a compreendê-la em toda sua complexidade. E assim, mergulhamos na busca pela significância de cada partícula que compõe essa misteriosa e fascinante substância chamada…
O que significa message?
O que significa message? - Uma incursão pelo significado da palavra que guarda consigo o poder de conectar, instruir e emocionar. Uma pequena palavra que carrega um imenso poder de comunicação, capaz de transcender fronteiras e tocar corações. Descubra como uma simples message pode mudar vidas.
Medicina
O que significa acidente vascular cerebral?
O cérebro, essa incrível e intricada máquina responsável por nossas emoções e…

Create an Amazing Newspaper
Siga-nos
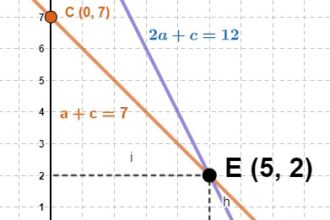
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
O que significa acumulação na matemática?
A acumulação é um conceito matemático fascinante que nos permite entender o…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CEP?
O CEP, ou Código de Endereçamento Postal, é uma seqüência numérica utilizada pelos Correios para facilitar a distribuição de correspondências e encomendas. Cada CEP corresponde a uma área específica, permitindo…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!