- Anúncios -
O que significa basketball?
O basketball é mais do que um simples jogo, é uma paixão que une nações ao redor do mundo. O que significa basketball? Significa superação, trabalho em equipe e habilidade. É o ritmo acelerado, a bola quicando no asfalto, os gritos de torcida e a sensação de estar voando. Basketball é amor, é emoção, é uma linguagem universal. É o…
O que significa being?
Você já se perguntou o que significa "being"? Essa palavra tão cheia de significados e complexidades pode ser difícil de definir. Mas o que é ser? Ser é existir, é observar, é sentir, é perceber. É estar presente no mundo, é se conectar com o universo. Ser é ser único, ser autêntico, ser humano. É viver, amar, aprender. É compreender…
O que significa budget?
A palavra "budget" é um termo inglês que vem sendo cada vez mais utilizado no vocabulário financeiro em português. Mas você sabe o que realmente significa? Descubra agora neste artigo e desvende os mistérios do mundo orçamentário.
Medicina
O que significa esquizofrenia?
A esquizofrenia é uma condição complexa que afeta a mente e a…

Create an Amazing Newspaper
Siga-nos
O que significa escalar na matemática?
Você já se perguntou o que significa escalar na matemática? Bem, imagine-se…
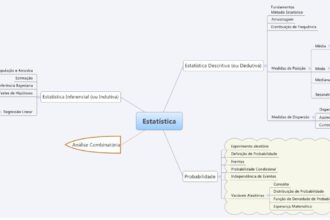
O que significa estatística na matemática?
A estatística na matemática é como uma lente que nos permite enxergar…
O que significa algoritmo?
Você já ouviu falar em algoritmo, mas sabe o que isso realmente…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…
O que significa seno na matemática?
O seno, um dos mais enigmáticos termos da matemática, desperta curiosidade e…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa algarismo na matemática?
O que significa algarismo na matemática? Quando nos deparamos com essa palavra…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CNPJ?
O CNPJ é um enigma envolto em números e siglas para muitos. Mas desvendemos esse mistério: CNPJ significa Cadastro Nacional da Pessoa Jurídica. É um número único que identifica as…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!