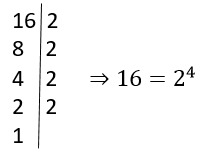- Anúncios -
O que significa unless?
O que significa unless? A palavra unless, em inglês, pode parecer um tanto intrigante para os falantes de português. No entanto, desvendar seu significado é como abrir uma caixa de surpresas linguísticas.
O que significa discipline?
O que significa disciplina? É um convite para olhar além das paredes da monotonia e explorar o poder transformador dessa palavra. É um chamado para a autodeterminação e o aprimoramento contínuo. É o fio condutor que nos impulsiona a alcançar nossos sonhos e objetivos mais ousados. Mas, acima de tudo, a disciplina é a habilidade de nos conhecermos verdadeiramente e…
O que significa sun?
O sol é a estrela que ilumina e aquece nosso planeta, proporcionando vida e energia. Em diversas culturas, ele é visto como um símbolo de poder, renovação e vitalidade. Descubra mais sobre o significado do sol e sua importância em nossa existência.
Medicina
O quê significar ser frugívoro?
Ser frugívoro é abraçar uma dieta baseada em frutas, reconhecendo sua importância…

Create an Amazing Newspaper
Siga-nos
O que significa denominador?
Você já se perguntou o que significa denominador? Uma palavra tão peculiar…
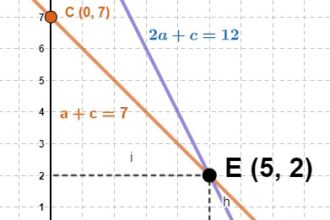
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa algoritmo?
Você já ouviu falar em algoritmo, mas sabe o que isso realmente…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
O que significa radiciação?
A radiciação é como um delicado desvendar, um mergulho profundo em busca…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SPED Contábil?
O SPED Contábil é um dos pilares do Sistema Público de Escrituração Digital no Brasil. Ele revolucionou a forma como as empresas reportam suas informações contábeis ao governo. Descubra o…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!