- Anúncios -
O que significa twin?
O que significa twin? Essa pequena palavra carrega consigo um grande mistério: a conexão única e inexplicável entre duas pessoas que compartilham a mesma data de nascimento. Os chamados gêmeos, ou "twins" em inglês, são seres fascinantes que despertam curiosidade e admiração. Vamos explorar esse mundo de simetria e união, onde os laços fraternais são levados a um novo nível.…
O que significa character?
Character é a essência de uma pessoa, representando seus valores, personalidade e moral. É a base para suas ações e decisões, definindo quem realmente são.
O que significa trial?
O que significa trial? Essa intrigante palavra, de origem inglesa, desperta nossa curiosidade e nos faz indagar seu real significado. Em sua essência, trial se refere a um período de teste ou experimentação, uma oportunidade para explorar novas possibilidades. Mas será que podemos aplicar esse conceito em diferentes áreas da nossa vida? Vamos desvendar esse enigma!
Medicina
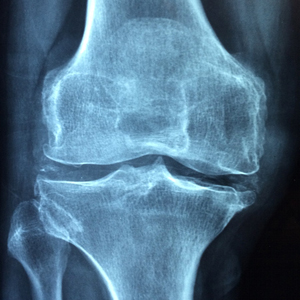
O que significa osteoporose?
Imagine uma teia de ossos frágeis, delicados como porcelana, que se quebram…

Create an Amazing Newspaper
Siga-nos
O que significa atrito na matemática?
Uma sensação de hesitação e resistência surge quando dois corpos se encontram,…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa coeficientes?
Mergulhando no mundo dos números, nos deparamos com os misteriosos coeficientes. Esses…
O que significa álgebra?
Um mundo de incógnitas e equações complexas, álgebra é um ramo fascinante…
O que significa equações polinomiais?
Você já se perguntou sobre o significado das equações polinomiais e como…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa BTW?
Você já se perguntou o que significa a sigla BTW? Se você é um entusiasta da internet, provavelmente já se deparou com essa expressão. BTW, ou "by the way", é…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!