- Anúncios -
O que significa walk?
O que significa walk? Apenas uma palavra de quatro letras, mas carregada de significado e possibilidades. Quando caminhamos, exploramos o mundo ao nosso redor, nos conectamos com a natureza e com nós mesmos. É um ato simples, porém poderoso, que nos leva além de limites físicos e nos liberta em busca de novas descobertas. Que tal calçar os sapatos e…
O que significa steady?
O termo "steady" é utilizado frequentemente no vocabulário da língua inglesa, mas o que ele realmente significa? "Steady" pode ser traduzido como "constante", "regular" ou "equilibrado". É uma palavra que expressa a ideia de estabilidade, consistência e confiabilidade. Se algo é "steady", podemos esperar que esse algo se mantenha firme, sem grandes variações. É como ter um navio navegando em…
O que significa how are you?
Quando alguém pergunta "How are you?" em inglês, significa simplesmente "Como você está?" Essa expressão é uma forma comum de cumprimento em países de língua inglesa.
Medicina
O que significa mieloma múltiplo?
Mieloma múltiplo, uma condição complexa e intrigante. Essa doença silenciosa é como…

Create an Amazing Newspaper
Siga-nos
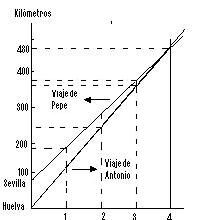
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa dividendo?
Você já se perguntou o que significa dividendo? Essa é uma palavrinha…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa multiplicação?
A multiplicação é como uma poção mágica matemática que transforma um número…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa FYI?
Sem dúvida, a sigla FYI já deve ter aparecido na sua caixa de entrada ou nas redes sociais. Mas o que ela realmente significa? FYI, abreviação de "for your information",…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!