- Anúncios -
O que significa telephone?
O que significa telephone? Esta palavra de origem francesa refere-se a um aparelho utilizado para comunicação à distância por meio de sinais elétricos. Saiba mais sobre a história e evolução deste dispositivo essencial nas nossas vidas modernas.
O que significa journey?
A jornada é mais do que uma simples viagem física, é uma jornada interna, transformadora e cheia de significado. Descubra o verdadeiro sentido da palavra "journey".
O que significa sanction?
A palavra "sanction" é daquelas que deixam muita gente intrigada. Surge logo a dúvida: o que significa? Na verdade, trata-se de um termo que carrega diferentes significados, mas que tem em comum o poder de impor penalidade ou restrição. Neste artigo, vamos explorar todas as nuances da palavra, para que você nunca mais fique perdido quando ela aparecer em um…
Medicina
O que significa anemia?
Anemia - a palavra que ecoa delicadamente no universo da saúde. Mas,…

Create an Amazing Newspaper
Siga-nos
O que significa matriz na matemática?
Matriz, um conceito tão simples, mas tão profundo. Como uma teia intrincada…
O que significa área na matemática?
Na matemática, a área é um conceito fundamental que nos permite medir…
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa coeficientes?
Mergulhando no mundo dos números, nos deparamos com os misteriosos coeficientes. Esses…
O que significa cosseno na matemática?
O cosseno é uma das grandezas fundamentais da matemática, mas seu significado…
O que significa escalar na matemática?
Você já se perguntou o que significa escalar na matemática? Bem, imagine-se…
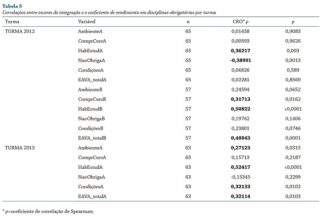
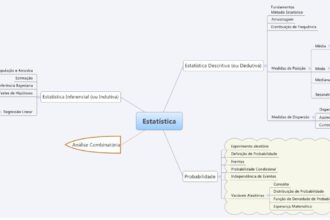
O que significa estatística na matemática?
A estatística na matemática é como uma lente que nos permite enxergar…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa PIS?
O Programa de Integração Social (PIS) é um benefício social oferecido aos trabalhadores brasileiros. Mas o que significa realmente PIS? Descubra nesse artigo que vai além das siglas e explora…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!