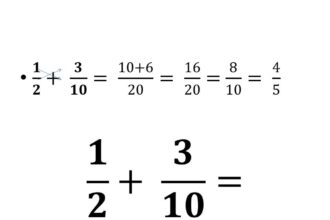- Anúncios -
O que significa rock?
O rock é muito mais do que um gênero musical. É uma atitude, uma forma de expressão que transcende barreiras culturais. O rock é rebeldia, é energia. É o som que fala diretamente à alma e faz o coração bater mais forte. O rock é um grito de liberdade, uma manifestação de identidade. Desde os seus primórdios até os dias…
O que significa overall?
No geral, a palavra "overall" em inglês possui diversos significados e abrange um espectro amplo de conceitos. Pode se referir a uma avaliação geral, à visão global de algo ou alguém, ou até mesmo às roupas conhecidas como macacões. De uma forma criativa, é uma palavra multifacetada que tanto nos permite compreender um todo como nos envolve em reflexões mais…
O que significa against?
Contra. Uma pequena palavra com um grande impacto. O que significa "against"? É um convite para a resistência, uma ode à persistência e uma celebração da diversidade de opiniões. É a voz dos que se colocam firmes em oposição, prontos para lutar pelos seus valores. É um lembrete de que, muitas vezes, o verdadeiro progresso surge quando nos opomos ao…
Medicina
O que significa hemofilia?
A hemofilia, essa misteriosa palavra, ecoa como um enigma nos corredores do…

Create an Amazing Newspaper
Siga-nos
O que significa associação na matemática?
Já se questionou sobre o que significa associação na matemática? Muito além…
O que significa logaritmo na matemática?
O logaritmo, um conceito matemático tão enigmático quanto fascinante, desvenda os segredos…
O que significa dividendo?
Você já se perguntou o que significa dividendo? Essa é uma palavrinha…
O que significa média na matemática?
Você já se perguntou o que significa média na matemática? A média…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa adição?
A adição, um conceito matemático fundamental, revela-se como um enigma estimulante para…
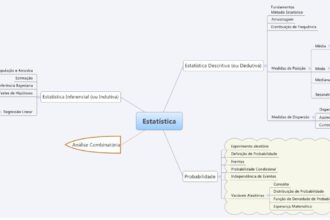
O que significa estatística na matemática?
A estatística na matemática é como uma lente que nos permite enxergar…
O que significa denominador?
Você já se perguntou o que significa denominador? Uma palavra tão peculiar…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa NVM?
Você provavelmente já se deparou com a famosa abreviação "NVM" nas mensagens de texto ou em chats online. Mas, afinal, o que significa NVM? Descubra aqui o significado dessa expressão…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!