- Anúncios -
O que significa authority?
Authority é um termo que evoca poder, controle e respeito. Significa possuir a legitimidade para exercer influência sobre outros, seja por conhecimento, posição social ou habilidade. A autoridade, entretanto, requer responsabilidade e ética para não se transformar em abuso. Compreender seu significado é fundamental para construir relações saudáveis e equilibradas em qualquer contexto.
O que significa survive?
Você já se perguntou o que significa sobreviver? É mais do que apenas existir. É resistir às adversidades, superar os obstáculos e encontrar força dentro de si mesmo. É explorar a coragem que existe em nosso âmago e enfrentar os desafios com determinação. Sobreviver é uma ode à resiliência humana, uma prova de que somos capazes de enfrentar as tempestades…
O que significa carroza em Espanhol?
O que significa carroza em espanhol?" é uma pergunta comum entre os estudantes de língua espanhola. Embora possamos imaginar uma carruagem decorada, a palavra também pode se referir a outros tipos de veículos festivos utilizados em desfiles ou festas tradicionais. Descubra mais sobre esse significado colorido e culturalmente rico da palavra "carroza" no idioma espanhol.
Medicina
O que significa ter sinusite?
Se você já acordou com o rosto dolorido, a respiração congestionada e…

Create an Amazing Newspaper
Siga-nos
Precisa ler
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa assíntota na matemática?
As assíntotas são como linhas invisíveis que atraem ou afastam uma curva,…
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa geometria na matemática?
Geometria, uma palavra que desperta curiosidade e desafia a imaginação. Na matemática,…
O que significa subtração?
A subtração é um conceito matemático que pode parecer complicado à primeira…
O que significa expressão numérica?
A expressão numérica, um enigma matemático envolto em símbolos, números e operações.…
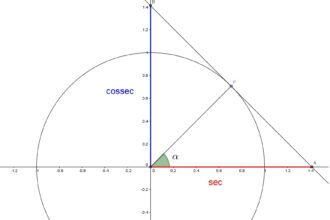
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa CPF?
CPF, a sigla que atormenta e confunde muitos brasileiros. Mas, afinal, o que significa CPF? São as iniciais de Cadastro de Pessoas Físicas, um número único e indispensável para a…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!