- Anúncios -
O que significa mind?
A mente, esse intrínseco e misterioso universo que habita em cada um de nós, transcende definições simples. O que é mente? É o fluir incessante de pensamentos, a criatividade que borbulha no âmago do ser, é a sede de conhecimento e a morada das emoções mais profundas. Encerra sonhos, desvenda segredos e molda nossa própria existência. No entanto, não há…
O que significa survive?
Você já se perguntou o que significa sobreviver? É mais do que apenas existir. É resistir às adversidades, superar os obstáculos e encontrar força dentro de si mesmo. É explorar a coragem que existe em nosso âmago e enfrentar os desafios com determinação. Sobreviver é uma ode à resiliência humana, uma prova de que somos capazes de enfrentar as tempestades…
O que significa compose?
Já se perguntou o que significa a palavra "compose"? Com uma origem que remonta ao latim, essa palavra pode ter diversos significados e usos. Do ato de escrever uma música à habilidade de combinar elementos em uma obra de arte, "compose" tem um mundo de possibilidades criativas esperando para serem exploradas. Descubra mais sobre esse termo fascinante e expanda seus…
Medicina
O que significa hemofilia?
A hemofilia, essa misteriosa palavra, ecoa como um enigma nos corredores do…

Create an Amazing Newspaper
Siga-nos
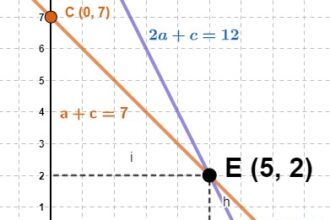
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
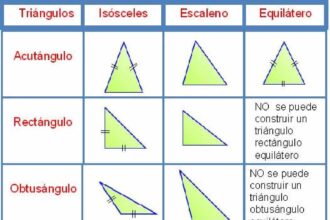
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa probabilidade na matemática?
A probabilidade sempre nos desafia com seu mistério matemático. Ela é um…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SMH?
SMH, sigla em inglês para "Shaking My Head", é uma expressão cada vez mais frequente nas redes sociais. Utilizada para expressar desaprovação, incredulidade ou desânimo, essa expressão ganhou popularidade entre…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!