- Anúncios -
O que significa nor?
O termo "nor" é uma interjeição que ganhou popularidade entre os jovens brasileiros. Embora sua origem seja incerta, seu significado é bastante peculiar: uma expressão ambígua que pode representar tanto admiração quanto descrença. O "nor" se tornou uma forma divertida de expressar surpresa ou dar ênfase a algo. É interessante observar como as gírias se renovam e se reinventam, trazendo…
O que significa interpret?
Interpretar é como dançar com as palavras, é captar a essência de um texto e transmiti-lo de forma única. É ser o mediador entre línguas e culturas, desvendando os mistérios da comunicação. O intérprete é um artista invisível, que dá vida aos diálogos e conecta pessoas através das palavras. Descubra agora o significado de interpretar e mergulhe nesse universo fascinante!
O que significa recall?
Recall é a ação de chamar de volta um produto que apresenta algum tipo de defeito ou que representa riscos à saúde do consumidor. O objetivo é garantir a segurança e a satisfação dos clientes.
Medicina
O que significa ter tuberculose?
O que significa ter tuberculose? Uma simples palavra que carrega consigo uma…

Create an Amazing Newspaper
Siga-nos
O que significa acima na matemática?
Na matemática, a palavra "acima" ganha um novo significado. Deixando de ser…
O que significa cálculo?
Cálculo, um termo que provoca curiosidade e talvez até um certo temor…
O que significa geometria?
Geometria, a palavra que une formas, linhas e figuras num mundo de…
O que significa divisão?
Ao falarmos sobre divisão, mergulhamos em um mundo repleto de possibilidades e…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
O que significa propriedades matemáticas?
Você já se perguntou o que significa propriedades matemáticas? Neste artigo, exploraremos…
O que significa equação diferencial na matemática?
Resolver equações diferenciais pode ser desafiador para muitos estudantes de matemática, mas…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
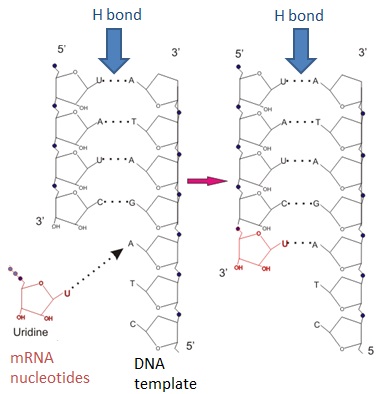
O que significa RNA?
Se você olhar para a própria essência da vida, vai se deparar com o RNA. Essas três letras representam uma das moléculas mais fundamentais e intrigantes da biologia. Mas o…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!