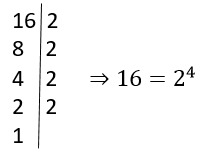- Anúncios -
O que significa respondent?
O termo "respondent" pode ser definido como uma pessoa que responde a alguma pergunta ou questionamento. Mas ele vai muito além disso! O respondent é aquele que traz vida e voz às pesquisas, compartilhando suas opiniões e experiências. É a peça fundamental para compreendermos o mundo ao nosso redor. Seja como parte de um estudo acadêmico ou de uma pesquisa…
O que significa mission?
A palavra "mission" traz consigo um senso inato de propósito e direção. Em português, mission pode ser traduzido como "missão", evocando um forte sentimento de busca por um objetivo ou cumprimento de uma tarefa designada. Seja no contexto religioso, empresarial ou pessoal, entender o significado de mission nos ajuda a encontrar nosso caminho e aspirações na vida.
O que significa detail?
O que significa detail? Essa palavra de origem inglesa pode ser traduzida como detalhe. No entanto, seu significado vai além do simples aspecto visual. Detail é a arte de observar minuciosamente, de atentar-se aos pequenos elementos que compõem algo, seja uma obra de arte ou um momento da vida. É perceber as nuances, as texturas, as sutilezas que tornam tudo…
Medicina
O quê significar ser antiinflamatório?
O quê significa ser antiinflamatório? É como um super-herói para o nosso…

Create an Amazing Newspaper
Siga-nos
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…
O que significa limite na matemática?
Na matemática, o limite é como uma fronteira que nos permite explorar…
O que significa isósceles?
O que significa isósceles? Essa palavra enigmática carrega consigo mistérios geométricos e…
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa seno na matemática?
O seno, um dos mais enigmáticos termos da matemática, desperta curiosidade e…
O que significa fórmula de Bhaskara na matemática?
A fórmula de Bhaskara, na matemática, é um marco que transcende a…
O que significa logaritmo na matemática?
O logaritmo, um conceito matemático tão enigmático quanto fascinante, desvenda os segredos…
O que significa equação?
O que significa equação? Quando mergulhamos no universo da matemática, nos deparamos…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa REINF?
Você já deve ter ouvido falar do termo REINF, mas você sabe o que realmente significa? O REINF é uma sigla que representa o Regime Especial de Regularização Cambial e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!