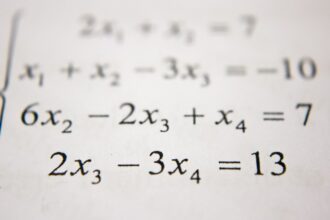- Anúncios -
O que significa piano?
Você já se perguntou o que significa a palavra "piano"? Derivada do termo italiano "pianoforte", que significa "suave e forte", o piano é um instrumento musical de teclas que permite aos músicos expressarem uma ampla gama de emoções através de suas melodias.
O que significa confident?
Confiança, a palavra tem um poder que ecoa além das definições. No entanto, quando se trata de "confident", sua tradução literal, "confiante", pode não expressar totalmente sua essência. Ser confident é transcender a autoconfiança, é irradiar segurança e impulsionar os outros. É um estado de espírito que instiga coragem e audácia. Então, quando se perguntarem: "O que significa confident?", lembre-se…
O que significa hearing?
Você já parou para se perguntar o que realmente significa a palavra "hearing"? O termo, que em inglês significa "audição", possui um significado rico e profundo que transcende os sons captados pelos nossos ouvidos. Neste artigo, exploraremos essa palavra de forma criativa, revelando as diversas nuances e camadas que envolvem o ato de ouvir. Definitivamente, o significado de "hearing" vai…
Medicina
O quê significar ser hiperglicídico?
Ser hiperglicídico significa ter um alto nível de glicose no sangue. Isso…

Create an Amazing Newspaper
Siga-nos
O que significa atrito na matemática?
Uma sensação de hesitação e resistência surge quando dois corpos se encontram,…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa média na matemática?
Você já se perguntou o que significa média na matemática? A média…
O que significa áreas de figuras geométricas?
Desde os tempos antigos, figuras geométricas têm sido um fascínio para os…
O que significa hipotenusa?
A hipotenusa é como aquele amigo que sempre dá o suporte necessário,…
O que significa operação matemática?
Mergulhando no colorido mundo da matemática, nos deparamos com a pergunta: o…
O que significa integral na matemática?
Você já se perguntou o que realmente significa "integral" na matemática? É…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa BRB?
Você provavelmente já encontrou essa sigla em conversas online e ficou se perguntando o que significa. BRB vem do inglês "be right back", ou seja, "volto já". Uma forma descontraída…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!