- Anúncios -
O que significa nut?
O que significa nut? Uma palavra curta, porém cheia de significado. Como uma semente que germina, nutrir é alimentar o corpo, a mente e a alma. Nutrir é cuidar, fortalecer, transformar. É encontrar o equilíbrio entre o conhecimento e a prática. Nutrir é saborear a vida em sua plenitude. Descubra os múltiplos significados dessa palavra e permita-se ser nutrido por…
O que significa wash?
O que significa "wash"? Essa pequena palavra de quatro letras tem o poder de nos transportar para um universo cheio de fragrâncias, texturas e limpeza. Mas será que seu significado vai além disso? Descubra agora o fascinante mundo por trás do verbo "wash" e mergulhe nessa jornada de conhecimento e suavidade.
O que significa action?
Action é uma palavra que pode ter diferentes significados dependendo do contexto em que é utilizada. Pode se referir a uma ação física, um movimento executado por alguém, ou também a uma iniciativa tomada para alcançar um objetivo específico. Em resumo, action representa a ideia de agir, de fazer algo acontecer.
Medicina
O que significa ter síndrome metabólica?
A síndrome metabólica é um conjunto de condições que colocam sua saúde…

Create an Amazing Newspaper
Siga-nos
O que significa integral na matemática?
Você já se perguntou o que realmente significa "integral" na matemática? É…
O que significa equações polinomiais?
Você já se perguntou sobre o significado das equações polinomiais e como…
O que significa potenciação?
Você provavelmente já se deparou com a potenciação em algum momento da…
O que significa vetor na matemática?
Quando entramos no mundo da matemática, nos deparamos com diversos conceitos e…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa acima na matemática?
Na matemática, a palavra "acima" ganha um novo significado. Deixando de ser…
O que significa função afim na matemática?
A função afim na matemática é como uma dança matemática encantadora, na…
O que significa equações exponenciais?
Você já se perguntou o que significam equações exponenciais? Essas equações misteriosas,…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
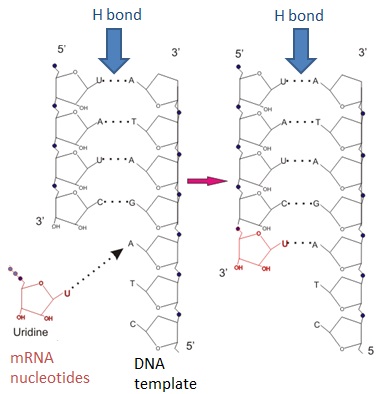
O que significa RNA?
Se você olhar para a própria essência da vida, vai se deparar com o RNA. Essas três letras representam uma das moléculas mais fundamentais e intrigantes da biologia. Mas o…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!