- Anúncios -
O que significa lower?
No vasto mundo dos idiomas, quando nos deparamos com a palavra "lower", seu significado pode trazer uma série de interpretações. Neste artigo, mergulharemos nas nuances dessa palavra, explorando seu sentido e contexto em diferentes situações. Prepare-se para desvendar os mistérios que "lower" pode nos revelar!
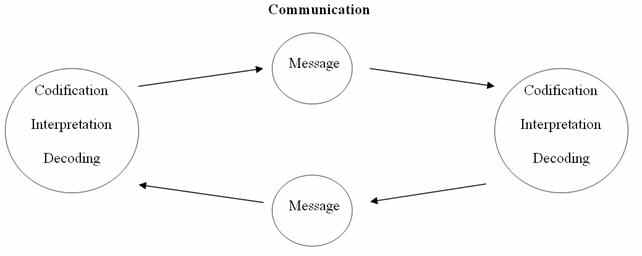
O que significa communication?
A comunicação é a linguagem dos seres humanos, o meio pelo qual expressamos nossos pensamentos, sentimentos e ideias. Ela transcende as palavras, é um intercâmbio de energias e conexões que nos conecta uns aos outros. É através da comunicação que podemos nos compreender, colaborar e criar relações significativas. Através da comunicação, revelamos nossa verdadeira essência e construímos o mundo ao…
O que significa judgment?
O que significa judgment? O termo pode ser definido como a capacidade de avaliar e formar opiniões sobre algo ou alguém. É um processo que envolve análise e discernimento para tomar decisões justas e equilibradas. Ajudando a distinguir entre o certo e o errado.
Medicina
O que significa ter rinite?
Rinite, uma viagem cheia de espirros e narizes entupidos. Mas afinal, o…

Create an Amazing Newspaper
Siga-nos
O que significa vetor na matemática?
Quando entramos no mundo da matemática, nos deparamos com diversos conceitos e…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…
O que significa equação de 2º grau?
A equação de 2º grau, também conhecida como equação quadrática, é um…
O que significa determinante na matemática?
O que significa determinante na matemática? O determinante é uma medida especial…
O que significa fórmula de Bhaskara na matemática?
A fórmula de Bhaskara, na matemática, é um marco que transcende a…
O que significa coeficientes?
Mergulhando no mundo dos números, nos deparamos com os misteriosos coeficientes. Esses…
O que significa propriedades matemáticas?
Você já se perguntou o que significa propriedades matemáticas? Neste artigo, exploraremos…
O que significa equação logarítmica?
Você já ouviu falar sobre equações logarítmicas? Essas expressões misteriosas podem parecer…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa OTAN?
A Aliança Atlântica, conhecida como OTAN, é um pacto militar que reúne diversos países do mundo ocidental. Mas afinal, o que significa OTAN? Neste artigo, vamos mergulhar nas origens e…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!