- Anúncios -
O que significa annual?
O termo "annual" remete a algo que ocorre anualmente, representa um ciclo ou evento que se repete a cada ano. Essa palavra desperta uma sensação de continuidade e regularidade, acompanhando o ritmo da natureza e da vida. No mundo dos negócios e finanças, é comumente utilizado para descrever relatórios e eventos que ocorrem uma vez por ano. Em resumo, "annual"…
O que significa continue?
O que significa continue? Uma palavra carregada de significados e possibilidades. Continue é a ponte entre o passado e o futuro, é a persistência que impulsiona o crescimento. É a voz interior que sussurra "não desista". Continue é a jornada que nunca acaba, o caminho que nos leva adiante. Continue é o combustível da determinação e o alimento da esperança.…
O que significa speaker?
O termo "speaker" refere-se a um dispositivo de áudio que converte sinais elétricos em ondas sonoras. Presente em muitos aparelhos, como caixas de som e smartphones, é essencial para a reprodução de áudio de qualidade.
Medicina
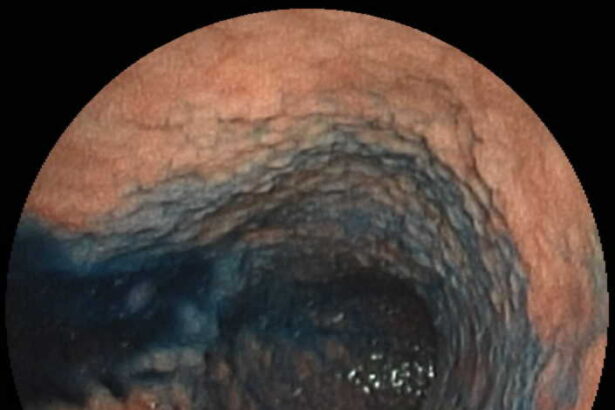
O que significa gastrite aguda ou crônica?
A gastrite aguda ou crônica é uma condição que afeta o revestimento…

Create an Amazing Newspaper
Siga-nos
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa equações irracionais?
Você já se perguntou o real significado das equações irracionais? Elas são…
O que significa adição?
A adição, um conceito matemático fundamental, revela-se como um enigma estimulante para…
O que significa multiplicação?
A multiplicação é como uma poção mágica matemática que transforma um número…
O que significa arco na matemática?
Na matemática, o arco é um elemento fundamental que nos leva a…
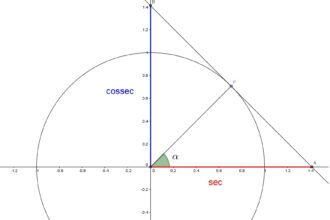
O que significa relações trigonométricas?
Você já se perguntou o que significa relações trigonométricas? Esses conceitos matemáticos,…
O que significa ângulo na matemática?
Na matemática, a palavra ângulo ganha vida própria. Ela se curva e…
O que significa algoritmo na matemática?
Algoritmo na matemática é como uma incrível coreografia numérica, uma dança entre…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa ROFL?
Você já se deparou com a famosa sigla "ROFL" nas redes sociais e não faz ideia do que significa? Não se preocupe, estamos aqui para te ajudar! "ROFL" é a…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!