- Anúncios -
O que significa tendency?
Tendência, um termo empreendedor tão enigmático quanto um labirinto encantado. Mas o que realmente significa? É como uma borboleta que pousa em nossas mentes, provocando curiosidade e incerteza. Como uma brisa suave, flutua entre o presente e o futuro, aflorando nosso desejo de compreender o imprevisível. Uma palavra com múltiplas camadas, repleta de mistério e fascínio. Afinal, a tendência não…
O que significa road?
As estradas avançam pela paisagem, serpenteando através dos montes e vales, conectando pessoas e lugares distantes. O que significa road? Para alguns, é o caminho que leva à aventura, enquanto para outros, é o conforto familiar de voltar para casa. Seja qual for o significado pessoal, é inquestionável que as estradas desempenham um papel crucial em nossas vidas, nos levando…
O que significa also?
Já se perguntou o que significa "also"? Esta pequena palavra é utilizada para adicionar informações ou enfatizar algo. Descubra mais sobre seu significado e como utilizá-la corretamente.
Medicina
O que significa ter encefalite?
Encefalite, um termo que ecoa nos corredores da medicina, desenterra uma complexidade…

Create an Amazing Newspaper
Siga-nos
O que significa equação logarítmica?
Você já ouviu falar sobre equações logarítmicas? Essas expressões misteriosas podem parecer…
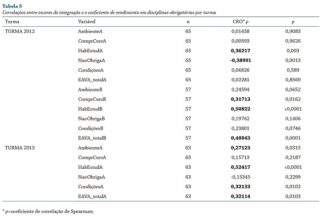
O que significa coeficientes?
Mergulhando no mundo dos números, nos deparamos com os misteriosos coeficientes. Esses…
O que significa estatística na matemática?
A estatística na matemática é como uma lente que nos permite enxergar…
O que significa vetor na matemática?
Quando entramos no mundo da matemática, nos deparamos com diversos conceitos e…
O que significa aproximação na matemática?
A aproximação na matemática é uma poderosa ferramenta que nos permite obter…
O que significa tangente na matemática?
A tangente, em sua essência matemática, é uma relação misteriosa entre duas…
O que significa volume na matemática?
O volume na matemática é uma dimensão mágica que transforma formas e…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa FYI?
Sem dúvida, a sigla FYI já deve ter aparecido na sua caixa de entrada ou nas redes sociais. Mas o que ela realmente significa? FYI, abreviação de "for your information",…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!