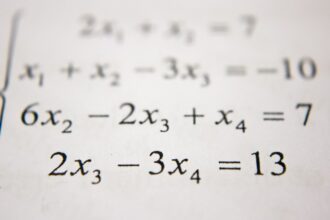- Anúncios -
O que significa disease?
A doença é como um enigma complexo que desafia nossa compreensão do corpo humano. Ela pode ser uma interrupção sutil ou uma batalha arrebatadora. Mas o que realmente significa a doença? Será que é apenas uma manifestação física dos desequilíbrios internos ou uma oportunidade para crescimento e autoconhecimento? Vamos explorar o significado por trás desse conceito e mergulhar nas profundezas…
O que significa native?
O que significa native? Uma palavra enigmática que desperta curiosidade e diversos significados. Em seu sentido mais básico, nativo pode referir-se àquilo que é original e próprio de um determinado lugar ou cultura. Mas além disso, native também pode ter conotações mais profundas, remetendo à essência e identidade de uma pessoa. Vamos explorar essa palavra rica e multifacetada que tanto…
O que significa piece?
O que significa piece?" é uma pergunta recorrente para os amantes da língua portuguesa. Literalmente, "piece" pode significar "pedaço". Porém, seu significado mais profundo vai além disso, levando em conta contexto e nuances. Vamos explorar essa "peça" do idioma em detalhes.
Medicina
O que significa ter mal de Alzheimer?
Ter mal de Alzheimer é como perder uma parte de si mesmo.…

Create an Amazing Newspaper
Siga-nos
O que significa equação diferencial na matemática?
Resolver equações diferenciais pode ser desafiador para muitos estudantes de matemática, mas…
O que significa fórmula de Bhaskara na matemática?
A fórmula de Bhaskara, na matemática, é um marco que transcende a…
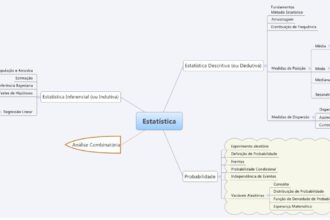
O que significa assunto na matemática?
Matemática, a pedra angular do conhecimento numérico, muitas vezes nos desafia com…
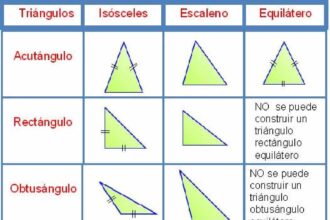
O que significa isósceles?
O que significa isósceles? Essa palavra enigmática carrega consigo mistérios geométricos e…
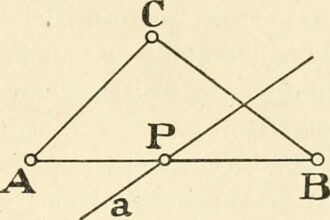
O que significa axioma na matemática?
Você já se perguntou o que significa axioma na matemática? Bem, prepare-se…
O que significa derivada na matemática?
Derivada na matemática é como uma chave mágica que nos permite desvendar…
O que significa média na matemática?
Você já se perguntou o que significa média na matemática? A média…
O que significa álgebra?
Um mundo de incógnitas e equações complexas, álgebra é um ramo fascinante…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa SISU?
Você já se perguntou o que significa SISU? Essa é uma sigla que representa o Sistema de Seleção Unificada, uma plataforma utilizada por diversas instituições de ensino superior no Brasil.…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!