- Anúncios -
O que significa be?
O que significa be?" é uma pergunta intrigante que surge na mente de muitos. Apreciando a simplicidade e a profundidade da palavra, é um convite à reflexão sobre sua essência e significado. Neste artigo, vamos explorar as diferentes interpretações e contextos desse termo enigmático, desvendando um pouco mais dos mistérios da língua portuguesa. Fique conosco e mergulhe nessa jornada de…
O que significa whisper?
O sussurro é como a brisa suave que acaricia o ouvido, um segredo sussurrado apenas para os ouvidos mais próximos. É a expressão mais íntima, um convite delicado para o intimacy humano. Descubra mais sobre o significado misterioso de "whisper".
O que significa accomplish?
Você sabe o que significa "accomplish" em português? Essa palavra, que pode ser traduzida como "realizar" ou "concluir", carrega consigo a ideia de alcançar metas, superar desafios e atingir sucesso. Com um significado tão poderoso, é importante entender como colocá-la em prática em nossa vida cotidiana. Venha descobrir mais sobre o significado e a importância de "accomplish" em nossas vidas.
Medicina
O que significa ter câncer?
O que significa ter câncer? Essa pergunta ecoa silenciosamente nos corações de…

Create an Amazing Newspaper
Siga-nos
O que significa trigonometria na matemática?
O que é a trigonometria? Para alguns, é o estudo dos números…
O que significa probabilidade na matemática?
A probabilidade sempre nos desafia com seu mistério matemático. Ela é um…
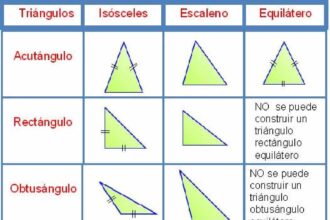
O que significa escaleno?
Escaleno, uma palavra que encerra mistério e equilíbrio. Entre os triângulos, este…
O que significa logaritmo na matemática?
O logaritmo, um conceito matemático tão enigmático quanto fascinante, desvenda os segredos…
O que significa logaritmação?
Você já se deparou com o termo "logaritmação" e ficou se perguntando…
O que significa argumento na matemática?
Na matemática, o termo "argumento" possui um significado peculiar. Ele refere-se à…
O que significa zero na matemática?
Zero na matemática: Um Portal para o Infinito Aquele número solitário que…
O que significa fator?
O fator, este enigma quase misterioso que permeia nosso universo matemático, representa…

Create an Amazing Newspaper
Conteúdo patrocinado
O que significa capitalismo?
O que significa capitalismo? É um conceito que se desdobra em um verdadeiro oceano de interpretações e debates. Desde sua origem na Revolução Industrial até os dias atuais, o capitalismo abrange os pilares da propriedade privada, da livre iniciativa e do mercado competitivo. Mas, será que esse sistema econômico tem se mostrado eficiente e sustentável para todos? Exploraremos essas questões e muito mais neste artigo, mergulhando nas profundezas desse complexo sistema que molda nossa sociedade contemporânea.
O que significa INSS?
INSS, o Instituto Nacional do Seguro Social, é um órgão brasileiro que tem como objetivo garantir proteção social aos cidadãos e promover o bem-estar. O nome pode parecer simples, mas…
Top Autores
Stay Up to Date
Subscribe to our newsletter to get our newest articles instantly!